树

树是由n(n>0)个有限节点组成一个具有层次关系的集合, 它具有以下特点:

每个节点有零个或多个子节点
没有父节点的节点叫做根节点
每个非根节点有且只有一个父节点
除了根结点外, 每个子节点可以分为多个不相交的子树

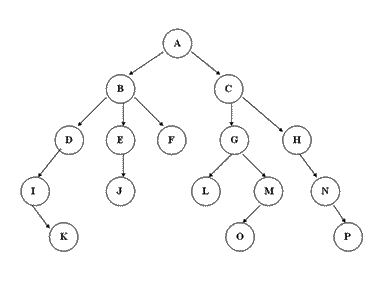
节点的度: 节点拥有的子树个树, 例如图中的节点A的度为2, 节点H的度为1

树的度: 树的最大节点的度, 例如图中最大的节点B的度为3, 树的度为3

叶节点: 度为0的节点, 图中K,J,F,L,O,P都是叶节点

父节点: 一个含有子节点的节点, 图中节点A就是节点B和节点C的父节点

子节点: 一个含有子树的根节点的节点, 把子树的根节点叫做该节点的子节点, 图中节点G和节点H为节点C的子节点

兄弟节点: 具有相同父节点的节点, 节点B和节点C就是兄弟节点

祖先节点: 从根到该节点所经分支的所有节点, 图中节点A,B,E是节点J的祖先节点

子孙节点: 以某节点为根结点的子树中所有节点, 图中节点D,E,F,I,J,K是节点B的子孙节点

节点层次: 从根开始, 根为第1层, 根的子节点为第2层…如果一个节点在第n层, 则它的子树的根结点在n+1层

深度或高度: 树中节点的最大层次, 例如图中的深度为5

森林: 由n颗互不相交的树的集合, 例如图中节点A去掉, 以节点B为根的树和以节点C为根的树组成的集合就叫做森林

二叉树

二叉树是每个节点最多只有两个子树的树结构, 这两种子树通常叫做左子树和右子树, 具有左右次序, 不能颠倒

二叉树的特点:

二叉树的第i层至多有2^(i-1)个节点(i>=1)
高度为h的二叉树至多有2^k-1个节点(h>=1)
非空二叉树中, 叶子节点树为n0, 分支度为2的节点数为n2, 则 n0 = n2 + 1
一颗高度为h且有2^k-1个节点的二叉树称为 满二叉树
高度为k, 有n个节点的二叉树, 当且仅当每个节点都可以和同高度的满二叉树, 序号为1到n一一对应时, 称为　完全二叉树

二叉树典型用法是对节点定义一个标记函数, 将一些值与每个节点相关系, 这样标记的二叉树可以实现 二叉搜索树 和 二元堆积 , 应用于高效率的搜索和排序

实现二叉搜索树

二叉搜索树有以下性质:

若任意节点的左子树不为空, 则左子树上所有节点的值都小于它的根节点的值
若任意节点的右子树不为空, 则右子树上所有节点的值都大于它的根节点的值
任意节点的左右子树也分别为二叉搜索树
没有值相等的节点

定义节点类和二叉树类

由二叉树的定义, 我们可以对节点定义代表存储左子树和右子树的属性

function Node(data) {
  this.data = data;
  this.leftChild = null;
  this.rightChild = null;
}

对二叉树来说, 定义一个根节点的属性

1
2
3

function BinaryTree() {
  this.root = null;  // 根结点
}

例如下图是Node环境下输出的二叉树结构, 一个对象嵌套着一个对象

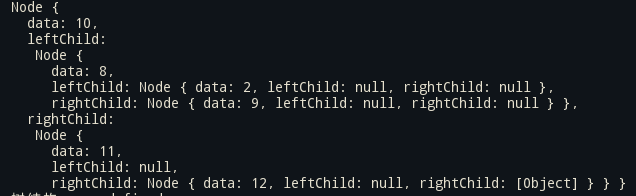
binary-tree-print

插入节点

由二叉搜索树的性质, 可以得到插入的过程:

二叉树为空, 新节点为根节点
二叉树不为空, 由根结点开始, 新节点的值小于当前节点, 往左子树递归, 若大于当前节点, 往右子树递归, 直到为null的时候插入

/**
 * @param  {object} node 当前节点对象
 * @param  {string} childName 构造函数Node中子树属性名称
 * @param  {object} newNode 新节点对象
 */
var insertChild = function(node, childName, newNode) {
  if (node[childName] === null) {
    node[childName] = newNode;
  } else {
    insert(node[childName], newNode);
  }
};

/**
 * 插入操作
 * 
 * @param  {object} node 当前节点对象
 * @param  {object} newNode 新节点对象
 */
var insert = function(node, newNode) {
  if (newNode.data < node.data) {
    insertChild(node, 'leftChild', newNode);
  } else {
    insertChild(node, 'right', newNode);
  }
};

/**
 * 二叉搜索树插入新节点调用方法
 * 
 * @param  {number} data 新节点的数值
 */
BinaryTree.prototype.inserNode = function(data) {
  var newNode = new Node(data);  // 构造Node的实例

  if (this.root === null) {  // 根节点为空, 新节点为根节点
    this.root = newNode;
  } else {
    insert(this.root, newNode);
  }
};

判断空树

判断是否是空树很简单, 当root为null时, 树就是空树, 返回true

BinaryTree.prototype.isBinaryTreeEmpty = function() {
  if (this.root) {
    return false;
  }

  return true;
}

二叉搜索树的高度(深度)

高度是树的最大层次, 可以用递归的方式, 分别计算左子树的高度和右子树的方式, 然后取它们之间最大值

var treeDepth = function(node) {
  var i, j;

  if (node === null) {  // 空树, 高度为0
    return 0;
  }

  if (node.leftChild) {  // 计算左子树高度i
    i = treeDepth(node.leftChild);
  } else {
    i = 0;
  }

  if (node.rightChild) {  // 计算右子树高度j
    j = treeDepth(node.rightChild);
  } else {
    j = 0;
  }

  return i > j ? i+1 : j+1;
};

/**
 * 返回二叉搜索树高度的调用方法
 */
BinaryTree.prototype.binaryTreeDepth = function() {
  return treeDepth(this.root);
}

遍历

遍历分为深度优先遍历和广度优先遍历, 其中先序,中序,后序遍历属于深度优先遍历的特例, 这里暂时采用了递归方式实现(非递归算法可借助栈实现), 在二叉树中, 广度优先遍历又称为层次遍历, 这里采用了队列实现

先序遍历

先序遍历的过程: 先访问根节点, 其次左子树, 最后右子树

var preOrderTraverseNode = function(node, callback) {
  checkCallback(callback);

  if (node) {
    callback(node);
    preOrderTraverseNode(node.leftChild, callback);
    preOrderTraverseNode(node.rightChild, callback);
  }
};

BinaryTree.prototype.preOrderTraverse = function(callback) {
  preOrderTraverseNode(this.root, callback);
};

checkCallback(callback)是检查callback参数是否为函数的方法

var checkCallback = function(callback) {
  if (!callback || typeof callback !== 'function') {
    throw ('Callback function error.');
  }
};

中序遍历

先序遍历的过程: 先访问左子树, 其次根节点, 最后右子树

var inOrderTraverseNode = function(node, callback) {
  checkCallback(callback);

  if (node) {
    inOrderTraverseNode(node.leftChild, callback);
    callback(node);
    inOrderTraverseNode(node.rightChild, callback);
  }
};

BinaryTree.prototype.inOrderTraverse = function(callback) {
  inOrderTraverseNode(this.root, callback);
};

后序遍历

先序遍历的过程: 先访问左子树, 其次根节点, 最后右子树

var postOrderTraverseNode = function(node, callback) {
  checkCallback(callback);

  if (node) {
    postOrderTraverseNode(node.leftChild, callback);
    postOrderTraverseNode(node.rightChild, callback);
    callback(node);
  }
};

BinaryTree.prototype.postOrderTraverse = function(callback) {
  postOrderTraverseNode(this.root, callback);
};

层次遍历(广度优先遍历)

层次遍历指的是同深度节点从左到右依次遍历, 借助队列, 从根节点开始, 入列, 判断队列是否为空, 若不为空, 队首出列, 将队首的左右子树根节点入列, 不断循环直至队列的元素全部出列

BinaryTree.prototype.levelOrderTraverse = function(callback) {
  var queue = [],
      e = null;

  checkCallback(callback);

  if (this.root) {
    queue.push(this.root);

    while(queue.length > 0) {
      e = queue.shift();
      callback(e);
      
      if (e.leftChild) {
        queue.push(e.leftChild);
      }

      if (e.rightChild) {
        queue.push(e.rightChild);
      }
    }
  }
};

结尾

这里主要简单地记录了实现一颗二叉搜索树的过程, 树结构的应用范围很广, 还有很多地内容并没有在这里提及, 在接下来的学习和工作当中, 再继续补充这一部分的内容, 本文所有实现的代码可以从Github中查看

Web developer

JS实现数据结构-树

树

二叉树