常用的排序算法

Posted on | Edited on | In

排序算法 是一种能将一串数据依照特定排序方式进行排列的一种算法

这里记录了七种常见的排序算法, 其中稳定的排序算法有冒泡排序, 插入排序, 归并排序, 不稳定的排序算法有选择排序, 希尔排序, 堆排序, 快速排序

冒泡排序

冒泡排序是最简单的排序算法, 它需要从数组第一位开始遍历, 每相邻的两位比较大小, 然后按照递增(或递减)的需求, 交换数字, 直至最大(或最小)移到最后一位, 然后排除排序好的一位, 也就是长度减一, 继续重复地前面的步骤直至排序完成

冒泡排序

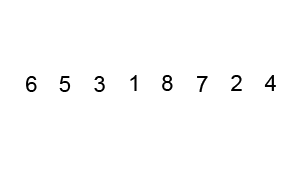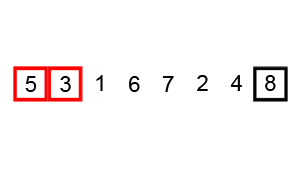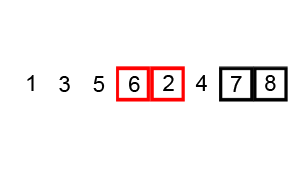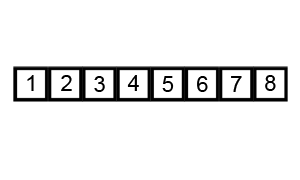
实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var swap = function(i, j, arr) {
  var temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
};

var bubbleSort = function(arr) {
  var len = arr.length,
      i = null,
      j = null;
  
  for (i = 0; i < len; i++) {
    for (j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j+1]) {
        swap(j, j+1, arr);
      }
    }
  }

  return arr;
};

时间复杂度: O(n^2)

空间复杂度: O(n)

鸡尾酒排序

鸡尾酒排序是冒泡排序的变形算法, 它与冒泡排序不同的是, 每排序好一位, 将反向继续进行排序

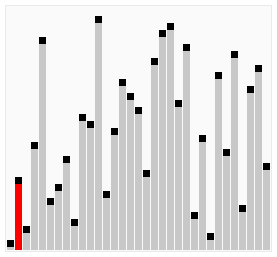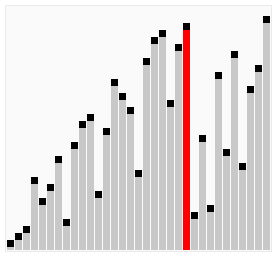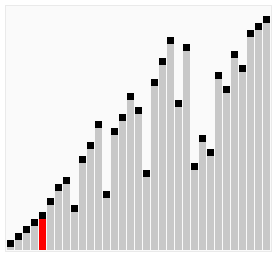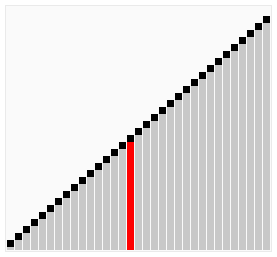
鸡尾酒排序

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
var CocktailSort = function(arr) {
  var head = 0,
      tail = arr.length - 1,
      i = null;
  
  while(head < tail) {
    for (i = head; i < tail; i++) {
      if (arr[i] > arr[i+1]) {
        swap(i, i+1, arr);
      }
    }
    
    tail--;

    for (i = tail; i > head; i--) {
      if (arr[i-1] > arr[i]) {
        swap(i-1, i, arr);
      }
    }

    head++;
  }

  return arr;
};

插入排序

插入排序指的是对未排序的数列, 依次从后向前在已排序的数列中找到相应的位置插入数据

插入排序

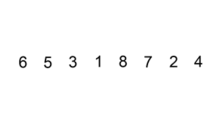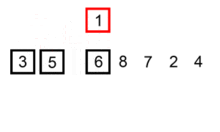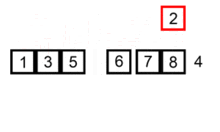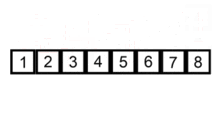
其运作过程:

  • 数组第一位看作是已排序好, 从下一位位开始进行向前扫描
  • 取出待插入数据, 从后向前比较数值大小, 若待插入数据小于对比数据, 对比数据向后移动一位，重复这一步骤直至待插入数据找到插入位置
  • 将待插入数据插入数组，循环继续进行直至数组排序完成

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var insertionSort = function(arr) {
  var len = arr.length,
      temp = null,
      i = null,
      j = null;
  
  for (i = 1; i < len; i++) {
    temp = arr[i];

    for (j = i - 1; j >=0 && arr[j] > temp; j--) {
      arr[j+1] = arr[j];
    }

    arr[j+1] = temp;
  }

  return arr;
};

时间复杂度: O(n^2)

空间复杂度: O(n)

归并排序

归并排序是将一组数列分组到最小单位, 再通过每相邻两组中的数值比较合并成一个有序的数列组, 不断地重复这个过程直至所有元素排序完成

归并排序

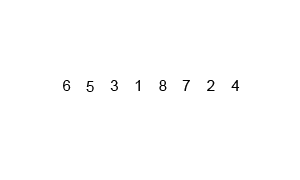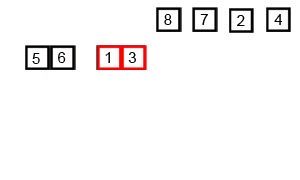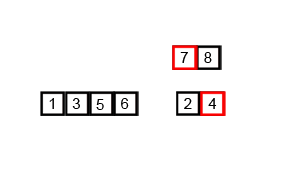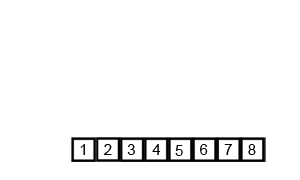
实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
var merge = function(left, right) {
  var result = [];

  while(left.length && right.length) {
    result.push(left[0] <= right[0] ? left.shift() : right.shift());
  }

  return result.concat(left.concat(right));
};

var mergeSort = function(arr) {
  var len = arr.length,
      midIdx = null,
      leftArr = [],
      rightArr = [];
  
  if (len < 2) {
    return arr;
  } else {
    midIdx = parseInt(Math.floor(len/2), 10);
  }

  leftArr = arr.slice(0, midIdx);
  rightArr = arr.slice(midIdx);

  return merge(mergeSort(leftArr), mergeSort(rightArr));
};

时间复杂度: O(nlogn)

空间复杂度: O(n)

选择排序

选择排序也是一种比较简单的排序算法, 它的运作原理是:

  • 先从未排序数列中找到最小(或最大)的数值, 将其放在未排序数列起始位置
  • 继续从剩下的未排序的数列中重复上面的过程

选择排序

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var selectionSort = function(arr) {
  var len = arr.length,
      index = null,
      i = null,
      j = null;
  
  for (i = 0; i < len; i++) {
    index = i;

    for (j = i + 1; j < len; j++) {
      if (arr[index] > arr[j]) {
        index = j;
      }
    }

    swap(index, i, arr);
  }

  return arr;
};

时间复杂度: O(n^2)

空间复杂度: O(n^2)

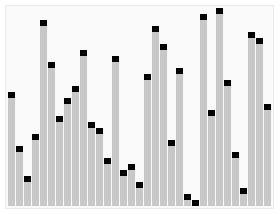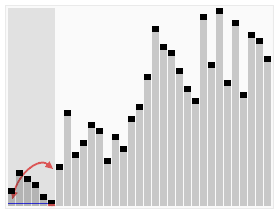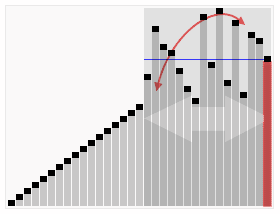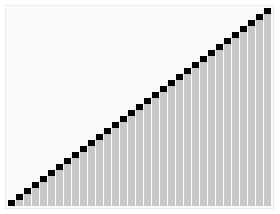
快速排序

快速排序是Javscript中sort方法实现的一种排序算法, 它使用分治法策略, 将数列分成两个子序列进行排序的过程, 具体运作原理为:

  • 从数列中取出一个基准数值
  • 将小于基准的数据放在左边, 大于基准的数据放在右边
  • 递归上面的步骤

快速排序

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var quickSort = function(arr) {
  var left = [],
      right = [],
      mid = arr[0];
    
  for (var i = 1; i < arr.length; i++) {
    if (arr[i] > mid) {
      right.push(arr[i]);
    } else {
      left.push(arr[i]);
    }
  }

  return quickSort(left).concat([mid], quickSort(right));
};

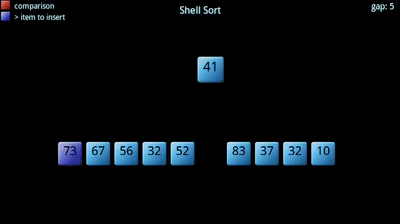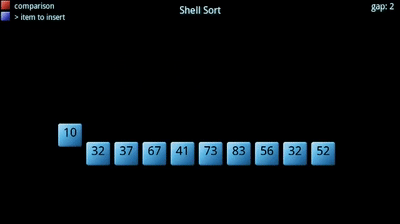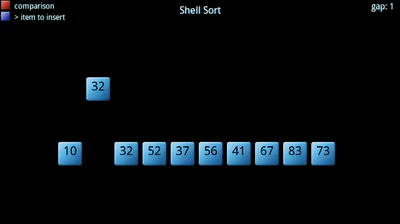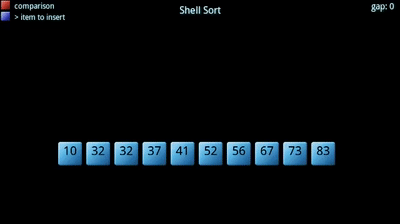
希尔排序

希尔排序是基于插入排序改进的一种算法, 插入排序对于几乎已排序的数列来说效率最高, 因此希尔排序在这个基础上, 通过将比较的全部数值分区域进行插入排序, 让一个数值可以一次性地移动更大的位置, 再不断地缩小步长直至1, 这时候大部分数据已排好序, 对于插入排序来说效率比较高

希尔排序

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var shellSort = function(arr) {
  var gap = Math.floor(arr.length/2),
      index = null,
      temp = null,
      i = null;
  
  while(gap > 0) {
    for (i = gap; i < arr.length; i++) {
      index = i - gap;
      temp = array[i];

      while(index >= 0 && arr[index] > temp) {
        arr[index+gap] = arr[index];
        index -= gap;
      }

      arr[index+gap] = temp;
    }

    gap = Math.floor(gap/2);
  }

  return arr;
};

时间复杂度: O(n)

空间复杂度: O(n)

堆排序

堆排序是利用堆的数据结构设计的一种排序算法, 堆有这近似完全二叉树的结构, 在一维数组中表示:

  • 父节点i的左子节点在位置2*i+1
  • 父节点i的右子节点在位置2*i+2
  • 子节点i的父节点在位置floor((i-1)/2)

在堆排序的操作中, 有:

  • 最大堆调整: 将堆的末端子节点作调整, 使子节点永远小于父节点
  • 创建最大堆: 将堆所有数据重新排序
  • 堆排序: 移除根结点, 并做最大堆调整递归运算

堆排序

实现代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
var maxHeapify = function(father, len, array) {
  var son = father*2 + 1,  // 左子节点的位置
      max = father;  // 父子节点中的最大值

  if (son >= len) {
    return;
  }

  if (son + 1 < len && array[son+1] > array[son]) {  // 如果右子节点(son+1)存在且大于左子节点
    son++;  // 取右子节点的位置
  }

  if (array[max] <= array[son]) {  // 父节点小于子节点, 交换
    swap(max, son, array);
    maxHeapify(son, len, array);
  }
};

var heapSort = function(arr) {
  var len = arr.length,
      i = null;
  
  // 创建最大堆
  for (i = Math.floor(len/2) - 1; i >= 0; i--) {
    maxHeapify(i, len, arr);
  }

  // 堆排序
  for (i = len - 1; i > 0; i--) {
    swap(0, i, arr);
    maxHeapify(0, i, arr);
  }

  return arr;
};

时间复杂度: O(nlogn)

空间复杂度: O(n)